5. Vectors

a. Definition, Magnitude and Direction

1. Vectors as Arrows

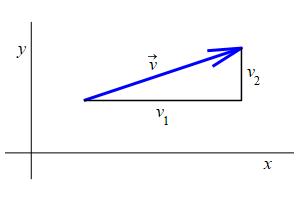
A vector is a quantity which has both magnitude and direction. It is useful to visualize the vector as an arrow in space pointing from its tail to its tip, but it is important to remember the vector is the arrow and it does not matter where we locate its tail. To emphasize the difference between vectors and numbers, we often use the word scalar to denote a number to emphasize that it is a single number which provides a size or scale, but with no associated direction in space. Also, we denote a vector by putting an arrow over its name, for example, \(\vec v\) and \(\vec a\) denote vectors, whereas \(v\) and \(a\) denote scalars or numbers.

Once we establish a rectangular coordinate system, a vector can be written as an ordered pair: \[\vec v=\left\langle v_1,v_2\right\rangle\] where \(v_1\) and \(v_2\) are called the components of \(\vec v\), and measure how much the \(x\)- and \(y\)-coordinates change as we move from the tail to the tip of the vector. But remember that vectors can start at any point, and not just at \((0,0)\).

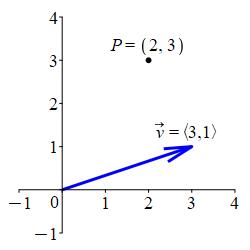
Notice that we use parentheses to surround the coordinates of a point but we use angle brackets to surround the components of a vector. For example, the plot shows the point \(P=(2,3)\) and the vector \(\vec v=\langle3,1\rangle\).

Vectors are useful in modeling properties of nature such as forces, velocities, and accelerations. In this course, we will study two-dimensional vectors. However, most of what we do will also work in \(3\) dimensions (by adding a component), as discussed in Calculus 3.

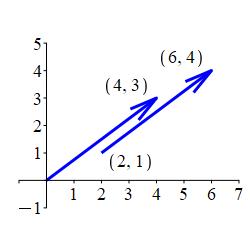
If the tail of the vector \(\left\langle4,3\right\rangle\) is located at the origin, \((0,0)\), then the tip is located at \((4,3)\). However, if the vector \(\left\langle4,3\right\rangle\) starts at \((2,1)\) then it ends at \((6,4)\).

In general, if the tail of the vector \(\vec v=\left\langle v_1,v_2\right\rangle\) is located at point \(P=(a,b)\), its tip would be at the point \(P+\vec v=(a+v_1,b+v_2)\). Two vectors are considered equal if they have the same direction and length no matter where they are located.

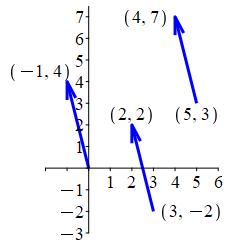
Consider the vector, \(\vec v\), from \((5,3)\) to \((4,7)\). Write the vector, \(\vec v\), in components. If it is moved so its tail is at \((3,-2)\), where will its tip be? If it is moved so its tail is at \((0,0)\), where will its tip be?

In components, the vector is \(\vec v=\left\langle-1,4\right\rangle\).
When its tail is at \((3,-2)\), its tip be will be at \((2,2)\).
When its tail is at \((0,0)\), its tip be will be at \((-1,4)\).

The vector from \((5,3)\) to \((4,7)\) has components which are the changes in the \(x\) and \(y\) coordinates. \[ \vec v=(4,7)-(5,3)=\left\langle-1,4\right\rangle \] When this vector is moved so its tail is at \((3,-2)\), its tip be will be at \[ (3,-2)+\left\langle-1,4\right\rangle=(2,2) \] When this vector is moved so its tail is at \((0,0)\), its tip be will be at \[ (0,0)+\left\langle-1,4\right\rangle=(-1,4) \]

Sometimes we want a vector to be located at a particular point, i.e. we want to specify where its tail is. For example a force may be applied to a particular point on an object. And sometimes we want to locate the vector at the origin.

A located vector is a vector together with a location for its tail.

If \(\vec v\) is a vector somewhere in space, then its position vector is the same vector \(\vec v\) but located at the origin. Notice that the tip of the position vector has the same coordinates as the components of \(\vec v\).

If the vector, \(\vec v=\left\langle3,-2\right\rangle\), is located at \((-1,5)\) then its tip will be at \[ (-1,5)+\left\langle3,-2\right\rangle=(2,3) \] Further, the tip of its position vector will be at: \[ (0,0)+\left\langle3,-2\right\rangle=(3,-2) \]

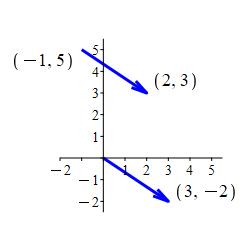
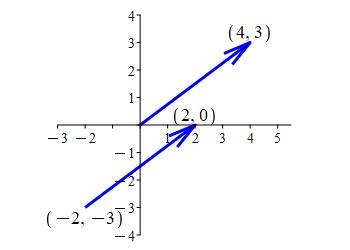
Consider the vector, \(\vec v\), from \((-2,-3)\) to \((2,0)\). What are the components of the vector? Where is the tip of its position vector?

The components of the vector are \(\vec v=\left\langle4,3\right\rangle\).
The tip of its position vector is \((4,3)\).

The components of the vector are the changes in the \(x\) and \(y\) coordinates: \[ \vec v=(2,0)-(-2,-3)=\left\langle4,3\right\rangle \] Its position vector is located at the origin. So its tip will be at \[ (0,0)+\left\langle4,3\right\rangle=(4,3) \]

5. Vectors

a. Definition, Magnitude and Direction

1. Vectors as Arrows

Heading